PITCH CLASS o SET THEORY

Método analítico

1. Enumeración de las alturas

Se basa en la contar el número de semitonos para abordar cualquier aspecto relacionado a la altura de la serie, melodía o armonía.

Segunda menor: 1 st	Quinta Justa: 7 st
Segunda Mayor: 2 st	Sexta menor: 8 st
Tercera menor: 3 st	Sexta Mayor: 9 st
Tercera Mayor: 4 st	Séptima menor: 10 st
Cuarta Justa: 5 st	Séptima Mayor: 11 st
Cuarta aumentada: 6 st	Octava: 12 st ó 0

La ordenación de sonidos se basa en el orden de aparición de la escala cromática en base al número 0. La transposición de octavas vendría reflejadas en la suma de mod. 12. Tn+12 (0+12= 12 Do octava) (0+24= 24 Do doble octava) (0-12= -12 Do octava baja) etc.

INTERVALO DE ALTURAS ORDENADO

Los intervalos de alturas entre dos puntos se mide en semitonos. Su fórmula es: ip (interval pitch) <x,y> = y-x. El intervalo existente entre x (primera nota) e y (segunda nota) será igual a la resta de y-x (Segunda nota menos la primera)

INTERVALO DE ALTURAS DESORDENADO

Parte de la misma idea anterior, pero en este caso no especificamos la dirección que toma el intervalo, sino únicamente la distancia entre las dos notas.

Así pues, si (14 – 6) = – 8 (8)

INTERVALO DE ALTURAS EN GRUPO CERRADO

El número resultante de la distancia del intervalo cuando éste es superior a 12 semitonos queda reflejado en módulo 12. Si el número es negativo se añade mod.12 a su valor.

INTERVALO DE ALTURAS DESORDENADAS EN GRUPO

Éste es el que resulta de la suma por el camino más corto utilizando un máximo de 6 semitonos.

i(a,b) es el camino más corto para el intervalo ofrecido en i<a,b> y i<b,a> Ordenamos el intervalo a el camino más corto. Si se obtienen números negativos deberá añadirse a aquel un número de 12 semitonos.

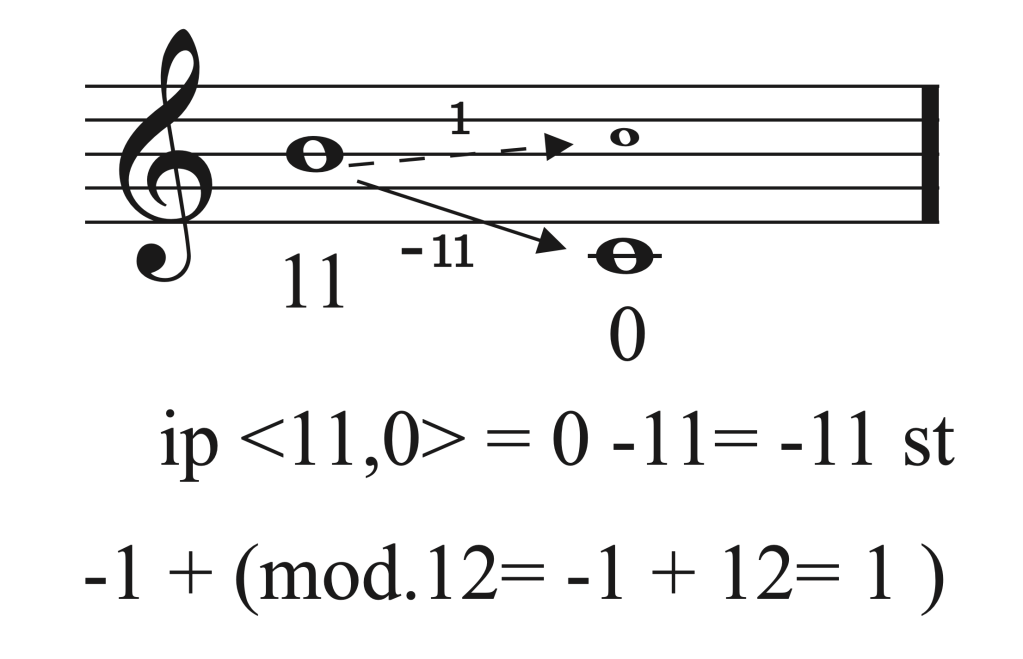
ORDEN EN GRUPO DE ALTURAS DE INTERVALOS

El orden de intervalos en un conjunto de notas es utilizado para dar coherencia al discurso musical desde un estudio analítico comprensible. Se deben distinguir los PC ordenados y desordenados. Por ejemplo, [0,2,3] se considera lo mismo que [2,3,0] no llegan a ser diferentes ya que contienen los mismos elementos. La única diferencia es el orden del que parten. En general se puede demostrar que existen tantas permutaciones como elementos se encuentran en un grupo de alturas. 1X, 2X, 3X, …Xn.

[a,b,c] [b,c,a] [c,b,a] — [a,b,c]…

[FORMA NORMALIZADA]

Debe ordenarse de forma ascendente con la menor diferencia entre el primer y último número entero. A los valores se les ha añadido 12st para ubicarlos de forma ascendente desde la rotación cuando ha sido necesario. Pueden recibir la misma numeración en módulo 12 aun estando escrito en distintas octavas.

a) [0,2,4,8] (8). b) [2,4,8,12] (10) c) [4,8,12,14] (10) d) [8,12,14,16] (8)

(FORMA PRIMARIA)

Dada una forma normalizada, ésta debe transponerse a Do. T0